SAM: A Segmentation based Approximate Multiplier for Error Tolerant Applications

Also Available Domains Arithmetic Core|Xilinx Vivado

Project Code :TVPGTO625

Abstract

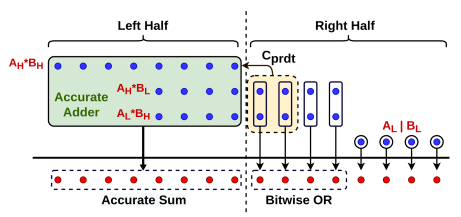
In this project, we propose a novel technique to multiply two unsigned binary numbers through a Segmentation based Approximate Multiplier (SAM). Approximate multiplier architectures face a fundamental challenge, i.e to reduce the area and delay significantly without introducing large inaccuracies. Almost all the existing approximate multipliers partition the input operands to exploit parallelism in the flow. The proposed design reduces the size of the Partial Products Matrix (PPM) in the order of n × (2n − 1) to a Reduced Partial Product Matrix (R-PPM) of the order 4 × 2n. Additionally, it also eliminates the extra hardware required for compression and rearrangement of partial products. µ-SAM, an optimized version of our basic design is also proposed along with this work. µ-SAM further minimizes the area and power consumption of the basic design.

NOTE: Without the concern of our team, please don't submit to the college. This Abstract varies based on student requirements.

Block Diagram

Specifications

Software Requirements:

Xilinx ISE Tool
HDL: Verilog

Hardware Requirements:

Microsoft® Windows XP,
Intel® Pentium® 4 processor or Pentium 4 equivalent with SSE support
512 MB RAM
100 MB of available disk space

Learning Outcomes

Basics of Digital Electronics
VLSI design Flow
Introduction to Verilog Coding
Different modeling styles in Verilog

Data Flow modeling
Structural modeling
Behavioral modeling
Mixed level modeling

Introduction to multiplier design
About Dadda multiplication
Knowledge on partial product generation and reduction
Knowledge on adders, compressors
About approximation computing
Applications in real time
Xilinx ISE 14.7 for design and simulation
Generation of Netlist
Solution providing for real time problems
Project Development Skills:

Problem Analysis Skills
Problem Solving Skills
Logical Skills
Designing Skills
Testing Skills
Debugging Skills
Presentation Skills
Thesis Writing Skills

Demo Video

Related Projects

Front End Domains

DSP Core
Communications and Crypto Core
Design for Testability
Nano Technology
Arithmetic Core

Back End Domains

Low Power VLSI
Transistor Logic
Core Memories

Tools

Tanner EDA
Xilinx ISE
Xilinx Vivado
Cadence EDA
FPGA

Others

Matlab Interfacing